Underfitting
When building a Machine Learning solution, you might end up with a model that shows poor results both on training and validation. Data Scientists face such a challenge occasionally and call it underfitting.
On this page, we will:
Define the underfitting term;
Explore the bias-variance tradeoff in Machine Learning;
Come up with a simple underfitting example;
Understand the potential reasons behind a model underfitting;
Learn how to detect underfitting early on;
And explore 5 ways of preventing and overcoming underfitting issues.
Let’s jump in.
What is Underfitting?
To define the term, underfitting is such a Machine Learning model behavior when the model is too simple to grasp the general patterns in the training data, resulting in poor training and validation performance. In other words, you can think of an underfitted model as "too naive" to understand the complexities and connections of the data.
Underfitting is not desirable model behavior, as an underfitted model is useless and cannot be used anywhere other than serving as a case in point, undermining the whole training point.
Let’s take a look at underfitting on a deeper level.
Bias-Variance tradeoff
The key to understanding underfitting lies in the bias-variance tradeoff concept. As you might know, when training an ML algorithm, developers minimize its loss, which can be decomposed into three parts: noise (sigma), bias, and variance.
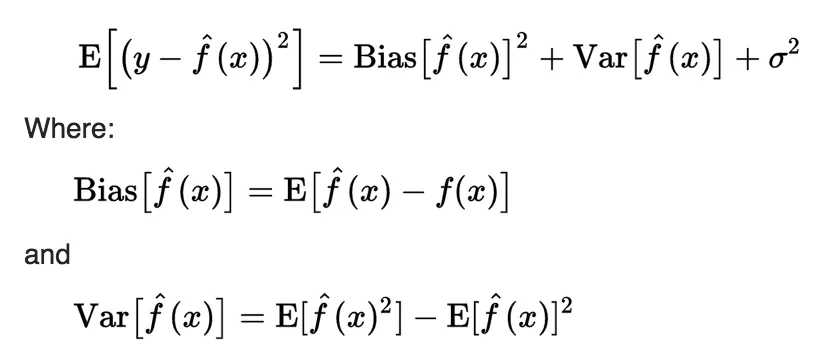
Source
Let’s get through them one by one:
The first component describes the noise in the data and is equal to the error of the ideal algorithm. There will always be noise in the data because of the shift from the training samples to real-world data. Therefore, it is impossible to construct an algorithm with less error;
The second component is the bias of the model. Bias is the deviation of the average output of the trained algorithm from the prediction of the ideal algorithm;
The third component is the variance of the model. Variance is the scatter of the predictions of the trained algorithm relative to the average prediction.
The bias shows how well you can approximate the ideal model using the current algorithm. The bias is generally low for complex models like trees, whereas the bias is significant for simple models like linear classifiers. The variance indicates the degree of prediction fluctuation the trained algorithm might have depending on the data it was trained on. In other words, the variance characterizes the sensitivity of an algorithm to changes in the data. As a rule, simple models have a low variance,
and complex algorithms - a high one.
Source
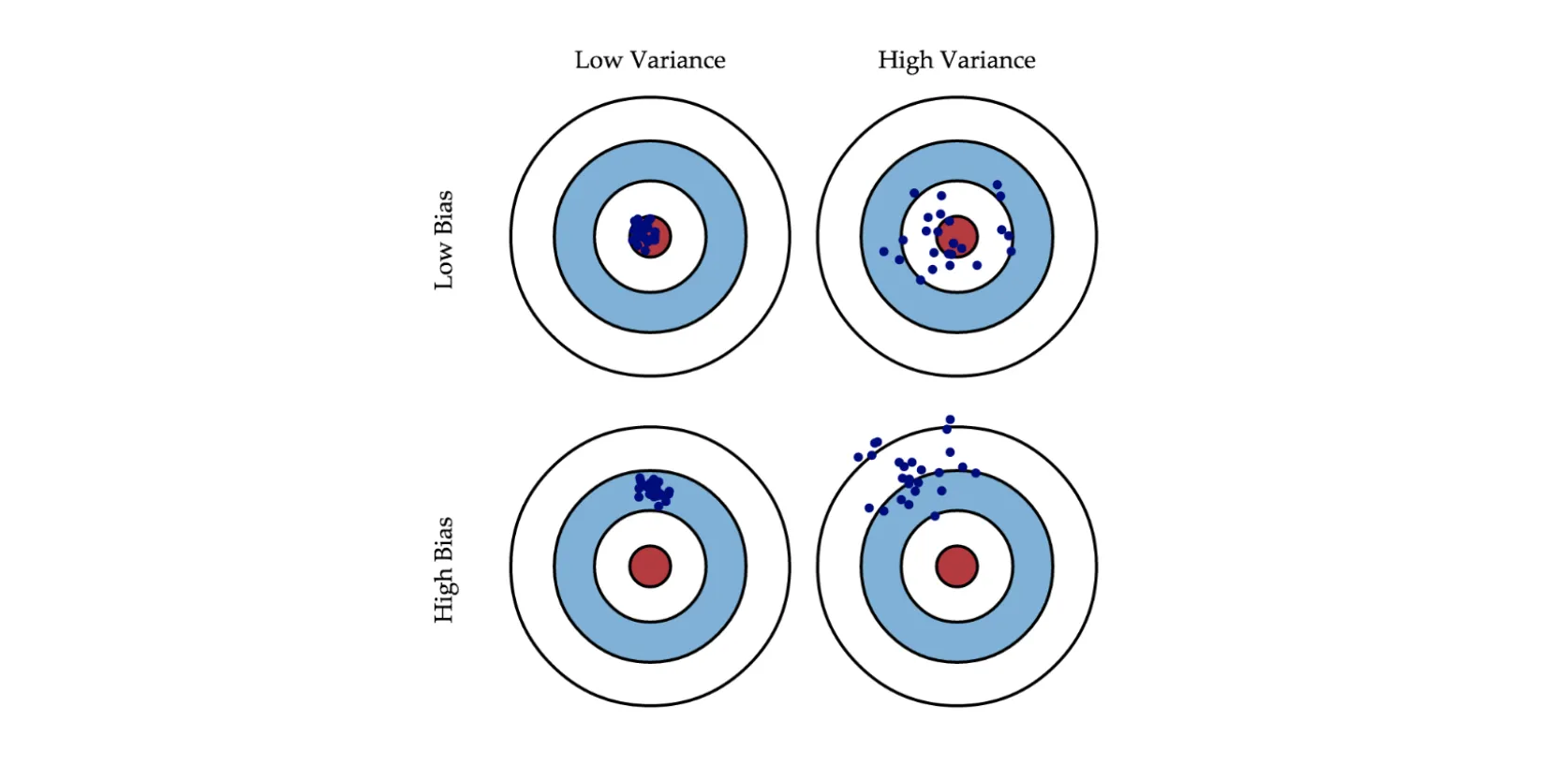
The picture above shows models with different biases and variances. A blue dot represents each model, so one dot corresponds to one model trained on one of the possible training sets. Each circle characterizes the quality of the model - the closer to the center, the fewer the model's error on the test set.
As you can see, having a high bias means that the model's predictions will be far from the center, which is logical given the bias definition. With variance, it is trickier as a model can fall both relatively close to the center as well as in an area with large error.
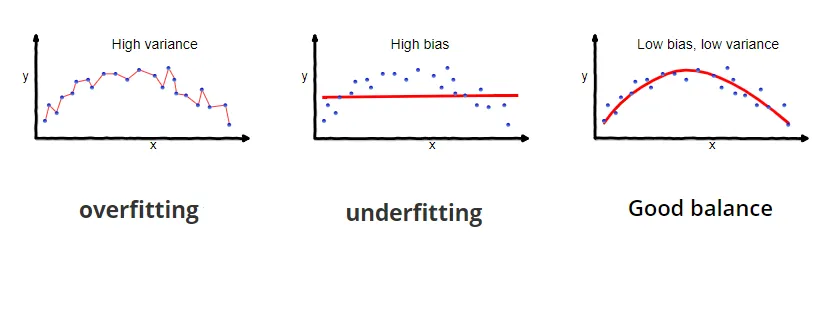
Bias and variance have an inverse relation: when bias is high, variance is low, and vice versa. This is well reflected in the image below.
Source
Thus, underfitting is such a scenario when the bias is so high that the model almost does not make any correct predictions, and the variance is so low that the model predicts samples very close to the average value.
Underfitting example
Let’s draw a simple underfitting example.
Imagine having the data with the parabolic dependence. The goal of your model is to learn to predict this relationship, but for some reason, you are using a model that can restore only linear dependencies. In such a case, you will get an underfitted model, as you can not force a linear model to learn how to predict non-linear dependencies between input and output.
Why does underfitting happen?
Underfitting reasons may vary from use case to use case. However, in general, you might want to check the following points.
Underfitting reason: Dirty dataset
If your dataset is noisy, contains plenty of outliers, or is preprocessed with mistakes, it might massively confuse the model and lead to underfitting, as the model will not have a chance to capture the general patterns in the data.
Underfitting reason: Very simple Machine Learning model
As shown above, a model will likely underfit if it is too basic for the complexity of the task or data. An example is training a linear regression model on a dataset with a high nonlinear relationship between the features and the target.
How to detect underfitting?
Underfitting is not something as easy to capture as overfitting. Technically, each model that is not 100% trained can be considered underfitted. But who decides that the model is well-trained? The answer is a Data Scientist who is just a human being that can make mistakes.
Therefore, below, we will mainly discuss the hardcore underfitting case when a model struggles massively to capture data patterns. There are different approaches to detecting an underfitting model. You can do it by checking the learning curves, empirically, or through cross-validation. Let’s check these methods one by one.
Underfitting detection: Learning curves
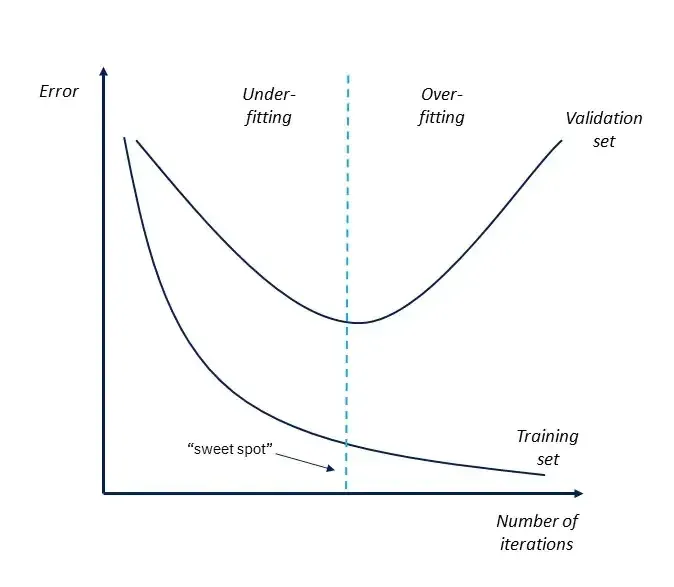
To diagnose the underfit, you can take a look at the model’s learning curves - the plot that reflects the model’s loss on the train and test data over iterations.
If the curves show a descending trend, your model is training. At some point, you might see that the training loss starts approaching zero while the validation loss suddenly rises. This is precisely where the model stopped extracting the general pattern (got fit) and started overfitting. So, the “sweet spot” to stop the training is right before the validation curve starts ascending.
Source
Underfitting detection: Empirical heuristic
An empiric way of detecting underfitting is by evaluating the Machine Learning performance on train and test steps. You will see poor performance in both stages with no visible life signs.
Underfitting detection: Cross-Validation
The most accurate approach to detecting underfitting (and other model weaknesses) is k-fold cross-validation. The algorithm is the following:
Shuffle your dataset and split it into k equal-sized folds;
Train your model on k - 1 folds and test its performance on the left-out fold;
Repeat the procedure k times so that each fold is used as a validation set once;
Take the average across the model’s performance on all the folds and analyze the obtained value.
How to prevent and overcome underfitting?
Underfitting is not as hot and vital as overfitting. Still, there are some valuable techniques to prevent and overcome underfitting in Machine Learning models and neural networks.
Some of these approaches are complex, so on this page, we will only draw a brief description of each method and leave links to more in-depth pages exploring a specific way.
For now, the most common techniques for dealing with underfitting are:
Increasing the model complexity. As mentioned above, a model might underfit because it is too simple. You can make it more complex (complicate its architecture or pick a more complex basic model) to try and overcome this;
Bringing more data. Introducing more training data can sometimes help, as it can expose the model to a broader range of patterns and relationships. However, this might not always be feasible or effective;
Decreasing the regularization strength. Regularization introduces additional terms in the loss function that punish a model for having high weights. Such an approach reduces the impact of individual features and forces an algorithm to learn more general trends. Besides traditional regularization techniques such as L1 and L2, in neural networks, weight decay and adding noise to inputs can also be applied for regularization purposes. In general, regularization is introduced to prevent overfitting, so to try and overcome underfitting, you should decrease the regularization strength;
More training time. This point is pretty much self-explanatory. You should give your model a bit more time to train and extract patterns while maintaining the balance between under- and overfitting;
Accurate preprocessing. As mentioned above, underfitting might occur because of a dirty dataset. Therefore, try a precise, organized, comprehensive preprocessing, including feature selection, feature engineering, data cleaning, and handling outliers. This might have a significant effect on the result.
These approaches provide a wide range of techniques to address underfitting issues and ensure better generalization capabilities of a model. The exact choice of a method depends significantly on the use case, data, model, goals, etc. Please explore the field before opting for a certain way.
Key takeaways: Underfitting
Underfitting is such a Machine Learning model behavior when the model fails to capture the patterns in the data, showing poor performance in the training and test stages.
The most accurate approach to detecting underfitting is k-fold cross-validation.
The general advice we can give you is to remember that underfitting exists, but techniques for overcoming it are there as well. Follow the simple five steps listed below to ease your life from underfitting when developing a Machine Learning solution:
Try to collect as diverse, extensive, and balanced a dataset as possible;
Keep track of the model learning curves to find the balance between underfitting and overfitting;
Do not use too complex or too simple models without the need for that;
Keep an eye on the strength of your regularization techniques;
Always validate your model performance on a set of examples not seen during training (for instance, using cross-validation).
These steps will not guarantee getting rid of underfitting for good. However, it is your responsibility and interest to make your model as reliable, robust, and generalizable as possible.
