Accuracy score
If you have ever tried solving a Classification task using a Machine Learning (ML) algorithm, you might have heard of the popular Accuracy score ML metric. On this page, we will:
- Сover the logic behind the metric (both for the binary and multiclass cases);
- Check out the metric’s formula;
- Find out how to interpret the Accuracy value;
- Talk about the disadvantages of the metric;
- Calculate Accuracy on a simple example (or two);
- And see how to work with the Accuracy score using Python.
Let’s jump in.
What is the Accuracy score in Machine Learning?
The most intuitive way to evaluate the performance of any Classification algorithm is to calculate the percentage of its correct predictions. And this is precisely the logic behind the Accuracy score.
To define the term, in Machine Learning, the Accuracy score (or just Accuracy) is a Classification metric featuring a fraction of the predictions that a model got right. The metric is prevalent as it is easy to calculate and interpret. Also, it measures the model’s performance with a single value.
So, to evaluate a Classification model using the Accuracy score, you need to have:
- The ground truth classes;
- And the model’s predictions.
Accuracy score formula
Fortunately, Accuracy is a highly intuitive metric, so you should not experience any challenges in understanding it. The Accuracy score is calculated by dividing the number of correct predictions by the total prediction number.
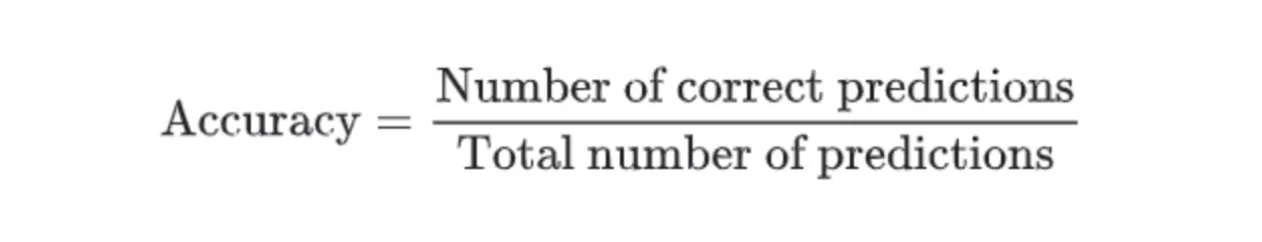
Source
The more formal formula is the following one.
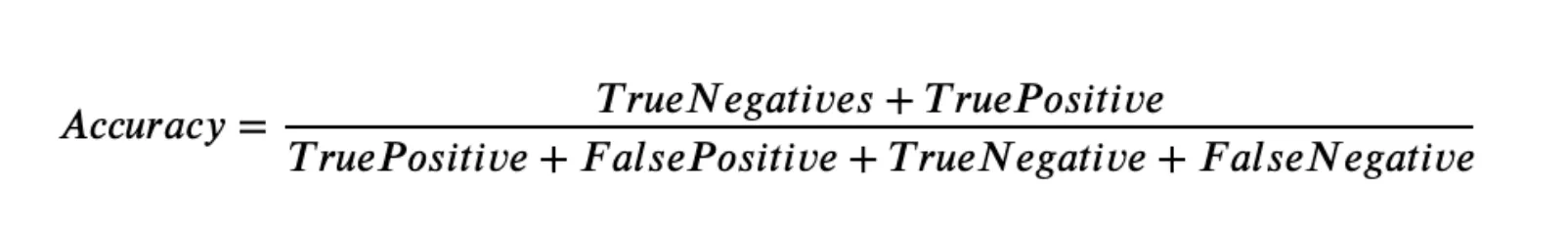
Source
As you can see, Accuracy can be easily described using the Confusion matrix terms such as True Positive, True Negative, False Positive, and False Negative. Still, as described on the Confusion matrix page, these terms are mainly used for the binary Classification tasks.
So, the Accuracy score algorithm for the binary Classification task is as follows:
- Get predictions from your model;
- Calculate the number of True Positives, True Negatives, False Positives, and False Negatives;
- Use the Accuracy formula for the binary case;
- And analyze the obtained value.
Yes, it is as simple as that. But what about the multiclass case? Well, there is no specific formula, so we suggest using the basic logic behind the metric to get the result. The Accuracy score algorithm for the multiclass Classification task is as follows:
- Get predictions from your model;
- Calculate the number of correct predictions;
- Divide it by the total prediction number;
- And analyze the obtained value.
Interpreting Accuracy score
In the Accuracy case, the metric value interpretation is more or less straightforward. If you are getting more correct predictions, it results in a higher Accuracy score. The higher the metric value, the better. The best possible value is 1 (if a model got all the predictions right), and the worst is 0 (if a model did not make a single correct prediction).
From our experience, you should consider Accuracy > 0.9 as an excellent score, Accuracy > 0.7 as a good one, and any other score as the poor one. Still, you can set your own thresholds as your logic and task might vary highly from ours (for example, in medicine, you might need to have an Accuracy score up to 0.99+ before calling a job done).
Still, this metric has two massive drawbacks that must be considered when using it. Let’s cover them one by one.
Accuracy score imbalance problem
The greatest problem is that Accuracy is utterly useless if the class distribution in your set is skewed. Let’s check out a simple example.
For example, we want to evaluate the performance of a mail spam filter. We have 100 non-spam emails. Our classifier correctly predicted 90 of them (True Negative = 90, False Positive = 10). From 10 spam emails classifier identified only 5 (True Positive = 5, False Negative = 5). In this case, the Accuracy score will be:
- Accuracy = (5 + 90) / (90 + 10 + 5 + 5) = 0.864
However, if we predict all emails as non-spam, we will get a higher Accuracy (True Negative = 100, False Positive = 0, True Positive = 0, False Negative = 10):
- Accuracy = (0 + 100) (0 + 100 + 0 + 10) = 0.909
The second model has a better metric value but does not have any predictive power. So, be very careful and always check whether your data has a class imbalance problem before applying Accuracy.
To be fair, Data Scientists came up with a solution to this problem by developing the Balanced Accuracy metric. Check its page in the sklearn documentation to learn more.
Accuracy score being uninformative
The other disadvantage is that Accuracy is not that informative when used as the only metric. For example, it does not tell you what types of errors your model makes.
At a 1% misclassification rate (99% Accuracy), the error could be caused by False Positives or False negatives. Such information is essential when evaluating a model for a specific use case. Take COVID tests as an example: you'd rather have FPs (the test says that a person has COVID, but he actually does not) than FNs (the test says that a person does not have COVID, but he actually does).
Overall, it is not a massive problem as you can solve it in a few lines of code by calculating some other metrics, but you still should keep in mind that relying only on the Accuracy value is a bad idea.
Accuracy score calculation example
Let’s say we have a binary Classification task. For example, you are trying to determine whether a cat or a dog is on an image. You have a model and want to evaluate its performance using Accuracy. You pass 15 pictures with a cat and 20 images with a dog to the model. From the given 15 cat images, the algorithm predicts 9 pictures as the dog ones, and from the 20 dog images - 6 pictures as the cat ones. Let’s build a Confusion matrix first (you can check the detailed calculation on the Confusion matrix page).
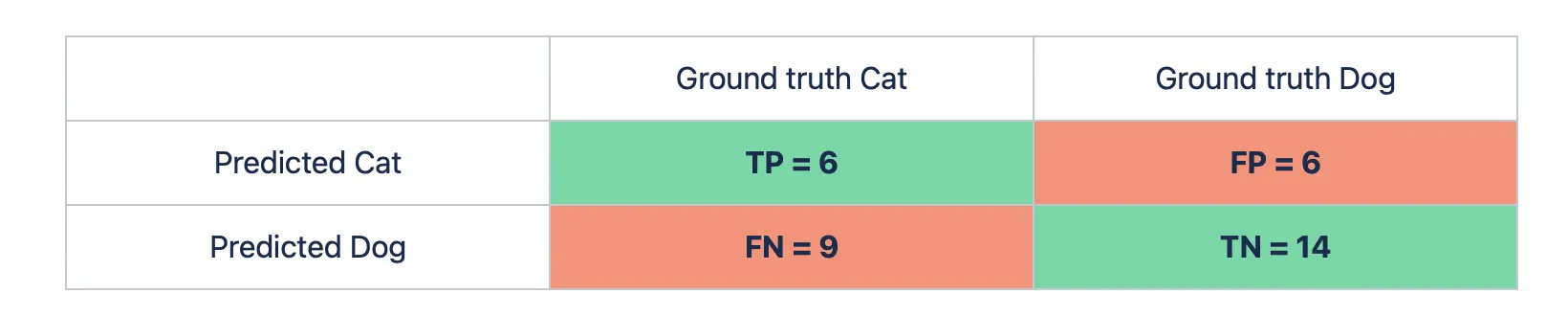
When it is done, the question arises...
How to calculate the Accuracy score from a Confusion matrix?
To calculate the Accuracy score from the Confusion matrix, try using the formula for the binary Classification task (the number of correct predictions is in the green cells of the table, and the number of incorrect ones is in the red cells).
- Accuracy = (TN + TP) / (TP + FP + TN + FN) = (14 + 6) / (6 + 6 + 14 + 9) ~ 0.57
Ok, great. Let’s expand the task and add another class, for example, the bird one. You pass 15 pictures with a cat, 20 images with a dog, and 12 pictures with a bird to the model. The predictions are as follows:
- 15 cat images: 9 dog pictures, 3 bird ones, and 15 - 9 - 3 = 3 cat images;
- 20 dog images: 6 cat pictures, 4 bird ones, and 20 - 6 - 4 = 10 dog images;
- 12 bird images: 4 dog pictures, 2 cat ones, and 12 - 4 - 2 = 6 bird images.
Let’s build the matrix.
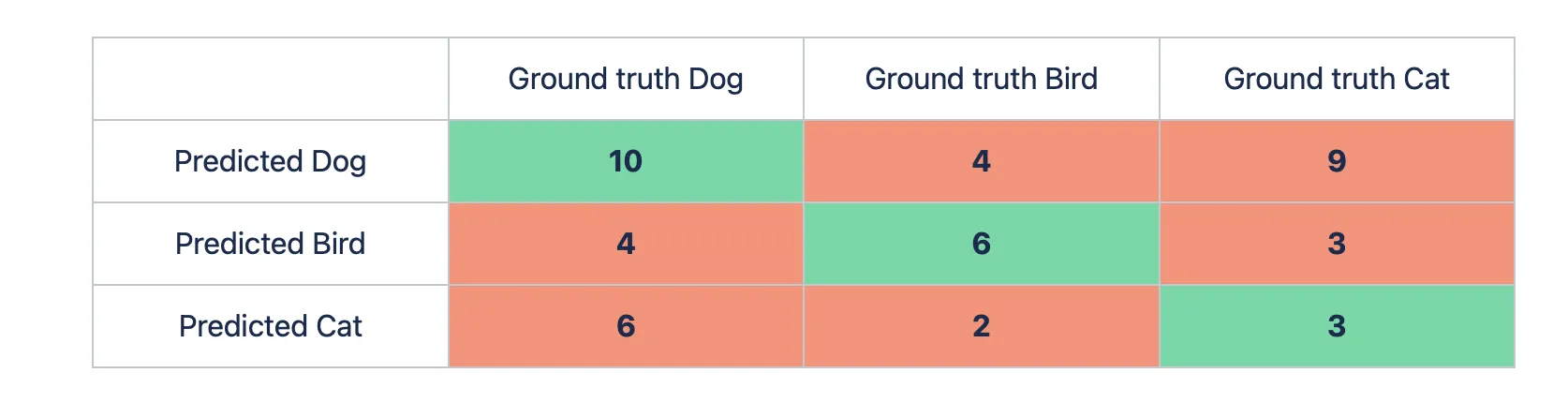
Let’s use the basic logic behind the Accuracy metric to calculate the value for the multiclass case.
- Number of correct predictions = 10 (dog) + 6 (bird) + 3 (cat) = 19;
- Total number of predictions = 10 + 4 + 9 + 4 + 6 + 3 + 6 + 2 + 3 = 47;
- Accuracy = 19 / 47 ~ 0.4
Accuracy score in Real-Life
As discussed above, while Accuracy is the most straightforward evaluation metric in Computer Vision, it is often misleading.
Its real-world applicability depends on class distribution, dataset balance, task complexity, and the cost of errors. In production, 99% of CV systems do not rely solely on the Accuracy score, as doing so can create false confidence in model performance — especially in imbalanced datasets and high-stakes applications.

Consider this example - an object detection system for a self-driving algorithm may achieve 99% Accuracy in pedestrian recognition if 99 out of 100 images contain no pedestrians. However, the 1% error rate could represent a life-threatening false negative, where a pedestrian goes undetected. Relying solely on Accuracy in this scenario would be a critical mistake, and the industry recognizes this limitation.
For instance, Volvo’s legacy research highlights the need to rely on multiple computer vision metrics but prioritize Recall in pedestrian detection. Missing a pedestrian has far more severe consequences than a false alarm, making a high Recall score essential for safety.
Accuracy score in Python
Accuracy score is widely used in the industry, so all the Machine and Deep Learning libraries have their own implementation of this metric. For this page, we prepared three code blocks featuring calculating Accuracy in Python. In detail, you can check out:
- Accuracy score in Scikit-learn (Sklearn);
- Accuracy score in TensorFlow;
- Accuracy score in PyTorch.
Accuracy score in Sklearn (Scikit-learn)
Scikit-learn is the most popular Python library for classical Machine Learning. From our experience, Sklearn is the tool you will likely use the most to calculate Accuracy (especially if you are working with tabular data). Fortunately, you can do it in just a few lines of code.
In Sklearn, Accuracy can be found under the accuracy_score function. The full path is sklearn.metrics.accuracy_score.
Beyond the basic functionality, Sklearn has various Accuracy options implemented. You should definitely check them out to simplify your workflow.
