Cross-Entropy Loss

Cross-entropy loss is a widely used alternative for the squared error. It is used when node activations can be understood as representing the probability that each hypothesis might be true, i.e., when the output is a probability distribution. Thus, it is used as a loss function in neural networks with softmax activations in the output layer.

Calculation / Interpretation

Cross entropy indicates the distance between what the model believes the output distribution should be, and what the original distribution really is.

$\$\$C.E=-\backslash sum\_i^C\; t\_i\; log(p\_i)\$\$$

Where $€€t\_i€€$ is the true label and $€€p\_i€€$ is the probability of the $€€i^\{th\}€€$ label.

The goal for cross-entropy loss is to compare how well the probability distribution output by Softmax matches the one-hot-encoded ground-truth label of the data.

It uses the log to penalize wrong predictions with high confidence stronger.

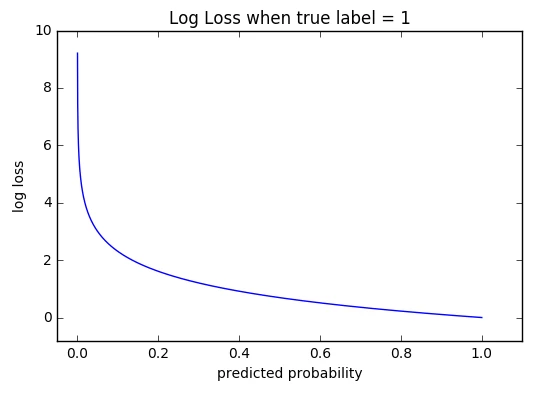
The cross-entropy loss function comes right after the Softmax layer, and it takes in the input from the Softmax function output and the true label.

Interpretation of Cross-Entropy values:

• Cross-Entropy = 0.00: Perfect predictions.
• Cross-Entropy < 0.02: Great predictions.
• Cross-Entropy < 0.05: On the right track.
• Cross-Entropy < 0.20: Fine.
• Cross-Entropy > 0.30: Not great.
• Cross-Entropy > 1.00: Terrible.
• Cross-Entropy > 2.00 Something is seriously broken.

Code implementation

PyTorch

      # importing the library
import torch
import torch.nn as nn

# Cross-Entropy Loss

input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)

cross_entropy_loss = nn.CrossEntropyLoss()
output = cross_entropy_loss(input, target)
output.backward()

print('input: ', input)
print('target: ', target)
print('output: ', output)
    

Further resources

• Binary Cross-Entropy Loss
• Classifiers